Huffman树与Huffman编码的Python实现

在之前的文章二叉树的Python实现和二叉搜索树（BST）的Python实现中，笔者分别介绍了二叉树与二叉搜索树的Python实现。本文将在此基础上，介绍Huffman树和Huffman编码的实现。

Huffman树

首先，我们先来看下什么是

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

其中涉及到的概念如下：

  • 树的带权路径长度（WPL）：树中所有叶子结点的带权路径长度之和
  • 结点的带权路径长度：是指该结点到树根之间的路径长度与该结点上权的乘积

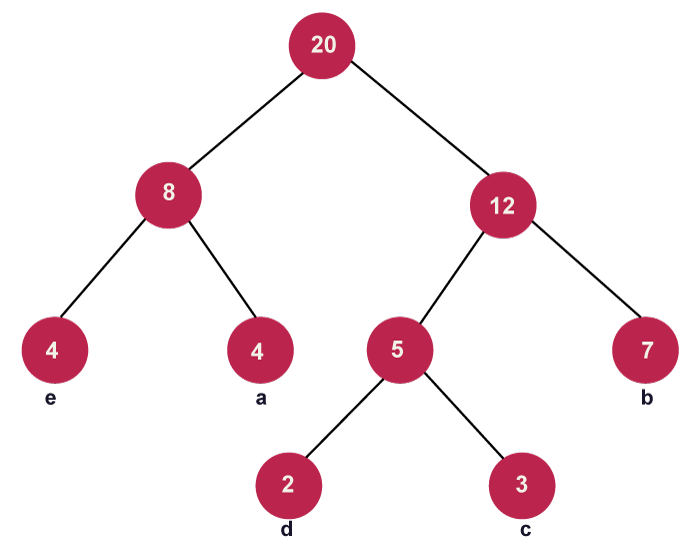
我们来看个例子：

叶子结点为a,b,c,d,e，图中这颗树的带权路径长度为

4 * 2 + 4 * 2 + 2 * 3 + 3 * 3 + 7 *2 = 45

那么，如何来构建Huffman树呢？

Huffman树的构造(Huffman Algorithm)算法如下：

  1. 根据给定的n个权值{w1,w2,…,wn}构成二叉树集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树为空；
  2. 在F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为左右子树根结点的权值之和；
  3. 在F中删除这两棵树,同时将新的二叉树加入F中；
  4. 重复2、3, 直到F只含有一棵树为止(得到哈夫曼树)。

利用我们之前实现的二叉树代码（参考文章 二叉搜索树（BST）的Python实现 中的二叉树实现代码），我们接着使用Python代码来实现Huffman树：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from binary_tree import BTree

values = [7, 19, 2, 6, 32, 3, 21, 10]
tree_list = [BTree(i) for i in values]

while len(tree_list) != 1:
    # 每个节点的数值
    values = [tree.data for tree in tree_list]
    # 从Node_list取两个节点数值最小的节点，并删除这两个节点
    min_value_tree = tree_list.pop(values.index(min(values)))
    values.pop(values.index(min(values)))
    sec_min_value_tree = tree_list.pop(values.index(min(values)))
    values.pop(values.index(min(values)))

    # 创建二叉树
    root_value = min_value_tree.data + sec_min_value_tree.data
    root = BTree(root_value)
    root.left = min_value_tree
    root.right = sec_min_value_tree

    # 在原来的Node_list中添加新的root节点
    tree_list.append(root)

root.print_tree(label=True)
# 前序遍历，中，左，右
root.pre_order()
print()
# 中序遍历，左，中，右
root.in_order()
print()
# 后序遍历，左，右，中
root.post_order()
print()
# 层次遍历
print(root.level_order())

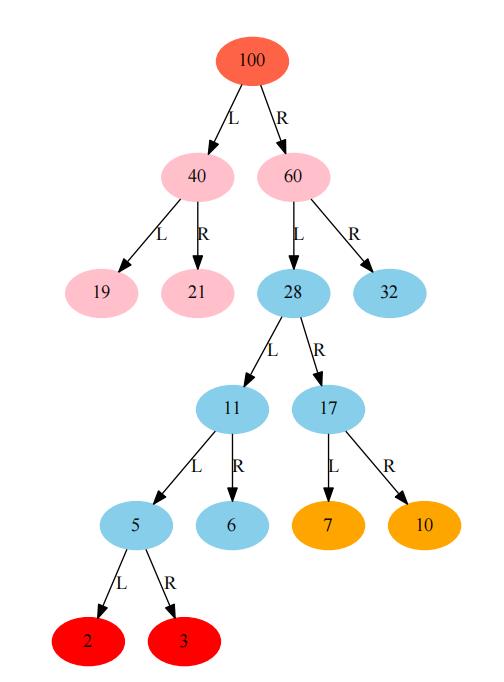
构建的Huffman树如下：

huffman tree

输出结果为：

1
2
3
4
100 40 19 21 60 28 11 5 2 3 6 17 7 10 32 
19 40 21 100 2 5 3 11 6 28 7 17 10 60 32 
19 21 40 2 3 5 6 11 7 10 17 28 32 60 100 
[[100], [40, 60], [19, 21, 28, 32], [11, 17], [5, 6, 7, 10], [2, 3]]

Huffman编码

Huffman树的一个重要应用是Huffman编码，而Huffman编码常用于数据解压缩。

Huffman coding

在实际使用Huffman数进行编码过程中，我们可以考虑对基本的文字单位（比如字母、汉字或者NLP中的token）按出现次数作为结点权重，去构建一颗Huffman树。此时，在这棵树中，以左子树路径为0，以右子树路径为1。

这样我们就能得到叶子结点的编码，此时该编码为前缀编码（任何一个字符的编码都不能是另一个字符编码的前缀）。

我们来看下面的例子（以字符串``为例）：

首先我们对二叉搜索树（BST）的Python实现中的二叉树进行改成，新增获取叶子结点方法以及二叉树可视化方法修改（将标签L, R改为0, 1），如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# @file: binary_tree.py
class BTree(object):
    # 初始化
    def __init__(self, data=None, left=None, right=None):
        self.data = data    # 数据域
        self.left = left    # 左子树
        self.right = right  # 右子树
        self.dot = Digraph(comment='Binary Tree')
        
    ...
    
    # 获取叶子节点
    @property
    def leaves(self):
        if self.data is None:
            return []
        if self.left is None and self.right is None:
            return [self]
        return self.left.leaves + self.right.leaves

    # 利用Graphviz进行二叉树的可视化
    def print_tree(self, save_path='./Binary_Tree.gv', label=False):

        # colors for labels of nodes
        colors = ['skyblue', 'tomato', 'orange', 'purple', 'green', 'yellow', 'pink', 'red']

        # 绘制以某个节点为根节点的二叉树
        def print_node(node, node_tag):
            # 节点颜色
            color = sample(colors,1)[0]
            if node.left is not None:
                left_tag = str(uuid.uuid1())            # 左节点的数据
                self.dot.node(left_tag, str(node.left.data), style='filled', color=color)    # 左节点
                label_string = '0' if label else ''    # 是否在连接线上写上标签，表明为左子树
                self.dot.edge(node_tag, left_tag, label=label_string)   # 左节点与其父节点的连线
                print_node(node.left, left_tag)

            if node.right is not None:
                right_tag = str(uuid.uuid1())
                self.dot.node(right_tag, str(node.right.data), style='filled', color=color)
                label_string = '1' if label else ''  # 是否在连接线上写上标签，表明为右子树
                self.dot.edge(node_tag, right_tag, label=label_string)
                print_node(node.right, right_tag)

        # 如果树非空
        if self.data is not None:
            root_tag = str(uuid.uuid1())                # 根节点标签
            self.dot.node(root_tag, str(self.data), style='filled', color=sample(colors,1)[0])     # 创建根节点
            print_node(self, root_tag)

        self.dot.render(save_path)      # 保存文件为指定文件

Huffman编码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
from binary_tree import BTree
from collections import Counter

# string字符串至少含有两个不同的字符
string = 'ABCACCDAEAE'
counter_dict = Counter(string)
print('各字符出现次数：', counter_dict)


# 返回一个数组的最小值，及其对应的下标
def min_and_index(array):
    f_minimum = float('inf')
    flag = None
    for i in range(len(array)):
        if array[i] < f_minimum:
            f_minimum = array[i]
            flag = i

    return f_minimum, flag


# create Huffman Tree
tree_list = [BTree(i) for i in counter_dict.values()]

while len(tree_list) != 1:
    # 每个节点的数值
    values = [tree.data for tree in tree_list]

    # 从Node_list取两个节点数值最小的节点，并删除这两个节点
    _, index = min_and_index(values)
    min_value_node = tree_list.pop(index)
    values.pop(index)
    _, index = min_and_index(values)
    sec_min_value_node = tree_list.pop(index)
    values.pop(index)

    # 创建二叉树
    root_value = min_value_node.data + sec_min_value_node.data
    root = BTree(root_value)
    root.left = min_value_node
    root.right = sec_min_value_node

    # 在原来的Node_list中添加新的root节点
    tree_list.append(root)
    values.append(root)

root.print_tree(label=True)

# print(root.leaves)

# Huffman Coding
queue = [root]

# node_dict: 节点及其对应的Huffman编码组成的字典
node_dict = {root: ''}
while queue:
    node = queue.pop(0)
    if node.left is not None:
        queue.append(node.left)
        node_dict[node.left] = node_dict[node] + '0'
    if node.right is not None:
        queue.append(node.right)
        node_dict[node.right] = node_dict[node] + '1'

# 叶子节点及其对应的Huffman编码
for node in root.leaves:
    print(node.data, '--->', node_dict[node])

# code_dict: 单个字符及其对应的Huffman编码
code_dict = {}
for char in counter_dict.keys():
    for node in root.leaves:
        if counter_dict[char] == node.data and node_dict[node] not in code_dict.values():
            code_dict[char] = node_dict[node]
            break

print(code_dict)

输出的结果为:

1
2
3
4
5
6
7
各字符出现次数： Counter({'A': 4, 'C': 3, 'E': 2, 'B': 1, 'D': 1})
2 ---> 00
1 ---> 010
1 ---> 011
3 ---> 10
4 ---> 11
{'A': '11', 'B': '010', 'C': '10', 'D': '011', 'E': '00'}

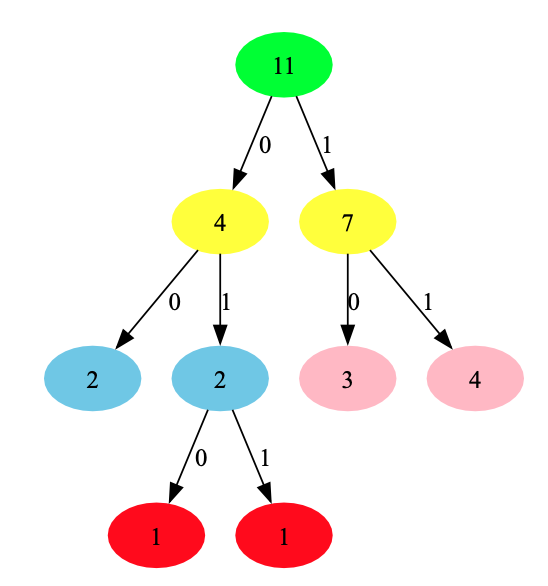
构建的Huffman树如下图：

构建的Huffman树

由上可知，对于各个字符的编码方式为：A=11, B=010, C=10, D=011, E=00.

观察上述的编码方式可知，这种编码方式是前缀编码（每个字母都是叶子结点，没有一个叶子结点在另一个叶子结点的路径上），因此可以用来做字符串的编解码。而且在满足前缀编码的前提下，Huffman编码的编码效率是最高的，即所用的0-1字符数最少，这就是Huffman编码的魅力。

这里，让我们停下脚步来想一想字符串编解码的问题。一种常见的编解码方式为等长编码，比如对于字符串ABCACCDAEAE，共5个字母，因此如果使用0-1编码的话，每个字符需使用3位编码，此时整个字符串需用11 * 3 = 33位编码，这种编码方式效率并不是最高的。

我们来看看Huffman编码的结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from math import floor, log2

# 对原字符串进行Huffman编码
coded_string = ''
for char in string:
    coded_string += code_dict[char]

print('压缩后的字符串为%s.' % coded_string)

# 一般方法的编码位数
if bin(len(counter_dict)).count('1') == 1 or len(counter_dict) == 1:
    bites = floor(log2(len(counter_dict)))
else:
    bites = floor(log2(len(counter_dict))) + 1

# print(bites)
# 一般方法的编码的总位数
original_code_bites = len(string) * bites
# 计算压缩比
ratio = original_code_bites/len(coded_string)

print('一般方法编码后的字符串长度为%s.' % original_code_bites)
print('Huffman编码后的字符串长度为%s.' % len(coded_string))
print('压缩比为%s.' % round(ratio, 3))

输出结果为：

1
2
3
4
5
{'A': '11', 'B': '010', 'C': '10', 'D': '011', 'E': '00'}
压缩后的字符串为110101011101001111001100.
一般方法编码后的字符串长度为33.
Huffman编码后的字符串长度为24.
压缩比为1.375.

而对于字符串'BCDEFGhHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'+'A'*10000000，其压缩比达到惊人的6.0。

Huffman decoding

有了Huffman编码，自然也需要对编码后的字符串进行解码。Huffman解码的思想是十分简单的，因为是前缀编码，对于编码后的字符串后，从头开始遍历，直到碰到叶子结点暂停，这样解码出一个字符，如此循环，直到编码后字符串结尾。

我们写一个示例的Huffman解码的Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
code_dict = {'A': '11', 'B': '010', 'C': '10', 'D': '011', 'E': '00'}
secret_string = "110101011101001111001100"

# Huffman Decoding
decoded_string = ''
while secret_string:
    for char, code in code_dict.items():
        if secret_string.startswith(code):
            decoded_string += char
            secret_string = secret_string[len(code):]
            break

print(decoded_string)

输出结果为ABCACCDAEAE。

注意观察，这样的解码代码效率是比较低的，使用了双重循环，对于长字符串的解码，效率是很低的。我们在本文的txt文件压缩实战部分来演示如何使用bitarray模块来提升Huffman解码效率，从而提升文件的编/解码效率。

其它用途

Huffman树和Huffman编码还有其他用途，其中之一便是刚才讲述过的文件编解码。其它用途列举如下：

  • 判别条件

对于如下的分类判别树（if-else条件）：

如果学生的总成绩数据有10000条，则5％的数据需 1 次比较，15％的数据需 2 次比较，40％的数据需 3 次比较，40％的数据需 4 次比较，因此 10000 个数据比较的次数为：

10000 (5％＋2×15％＋3×40％＋4×40％)＝31500次

而如果使用Huffman数，则可将判别次数减少至22000次，这样可以提升判别树的效率。

  • word2vec

在NLP中的word2vec算法（一种用于获取词向量的算法）中，对从隐藏层到输出的softmax层这里的计算量进行了改进。为了避免要计算所有词的softmax概率，word2vec采样了霍夫曼树来代替从隐藏层到输出softmax层的映射。

这是Huffman树在NLP领域中的一个精彩应用！

txt文件压缩实战

ok，讲了这么多，我们来看看Huffman编码在文件压缩领域中的作用（也是它的主战场）了。

在这里，我们使用Python中的bitarray模块来提升Huffman编/解码的效率。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
import json
from binary_tree import BTree
from collections import Counter
from bitarray import bitarray

# string字符串至少含有两个不同的字符
with open('test2.txt', 'r') as f:
    string = f.read()
print('原始文件中的前100个字符：', string[:100])
counter_dict = Counter(string)
print(counter_dict)


# 返回一个数组的最小值，及其对应的下标
def min_and_index(array):
    f_minimum = float('inf')
    flag = None
    for i in range(len(array)):
        if array[i] < f_minimum:
            f_minimum = array[i]
            flag = i

    return f_minimum, flag


# create Huffman Tree
tree_list = [BTree(i) for i in counter_dict.values()]

while len(tree_list) != 1:
    # 每个节点的数值
    values = [tree.data for tree in tree_list]

    # 从Node_list取两个节点数值最小的节点，并删除这两个节点
    _, index = min_and_index(values)
    min_value_node = tree_list.pop(index)
    values.pop(index)
    _, index = min_and_index(values)
    sec_min_value_node = tree_list.pop(index)
    values.pop(index)

    # 创建二叉树
    root_value = min_value_node.data + sec_min_value_node.data
    root = BTree(root_value)
    root.left = min_value_node
    root.right = sec_min_value_node

    # 在原来的Node_list中添加新的root节点
    tree_list.append(root)
    values.append(root)

# Huffman Coding
queue = [root]

# node_dict: 节点及其对应的Huffman编码组成的字典
node_dict = {root: ''}
while queue:
    node = queue.pop(0)
    if node.left is not None:
        queue.append(node.left)
        node_dict[node.left] = node_dict[node] + '0'
    if node.right is not None:
        queue.append(node.right)
        node_dict[node.right] = node_dict[node] + '1'

# code_dict: 单个字符及其对应的Huffman编码
code_dict = {}
for char in counter_dict.keys():
    for node in root.leaves:
        if counter_dict[char] == node.data and node_dict[node] not in code_dict.values():
            code_dict[char] = node_dict[node]
            break

# 对原字符串进行Huffman编码
coded_string = ''
for char in string:
    coded_string += code_dict[char]

# write the result to a file
with open('test2.bin', 'wb') as f:
    bitarray(coded_string).tofile(f)

# write the code_dict to a json file
with open('code_dict.json', 'w') as f:
    json.dump(code_dict, f)

输出结果为（由于篇幅原因，counter_dict变量只显示了前几个字符）:

1
2
原始文件中的前100个字符： 凡人修仙传 第二千三百零一章-第二千三百五十章 第两千三百零一章 再见灵王 话音刚落，他也不等一干空鱼人再说什么，就一张口，喷出那颗山海珠。 此珠方一飞出，立刻迎风滴溜溜的转动而起，一抹艳丽霞光从上面
Counter({'，': 8278, '一': 5472, '的': 5226, '。': 4718, ' ': 3260, '了': 2659, '不': 1929, '道': 1545, '是': 1543, '在': 1362, '这': 1287, '人': 1284, '”': 1283, '大': 1270})

原始文件test2.txt大小为453K，而编码后的test2.bin文件大小为166K，压缩效果较好。如果我们使用Linux中的tar命令: tar -zcvf test2.tar.gz test2.txt，压缩后的test2.tar.gz文件大小为183K。

接下来，我们使用code_dict.json对test2.bin进行Huffman解码，示例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import json
from bitarray import bitarray

# read json file
with open('code_dict.json', 'r') as f:
    code_dict = json.loads(f.read())

string = bitarray()
with open('test2.bin', 'rb') as fh:
    string.fromfile(fh)

secret_string = string[:len(string) - 8] + bitarray(string[len(string) - 8:].to01().strip('0'))
new_code_dict = {key: bitarray(value) for key, value in code_dict.items()}

# Huffman decoding effectively
dec = secret_string.decode(new_code_dict)
print('编码文件解码后的前100个字符：', ''.join(dec)[:100])

输出结果为：

1
编码文件解码后的前100个字符： 凡人修仙传 第二千三百零一章-第二千三百五十章 第两千三百零一章 再见灵王 话音刚落，他也不等一干空鱼人再说什么，就一张口，喷出那颗山海珠。 此珠方一飞出，立刻迎风滴溜溜的转动而起，一抹艳丽霞光从上面

与原始文件一致。

总结

总结下，本文主要介绍了Huffman树和Huffman编码的原理和Python代码，并介绍了他们的用途，最后再介绍了txt文件压缩实战。

参考文献

  1. 霍夫曼编码: https://zh.wikipedia.org/wiki/%E9%9C%8D%E5%A4%AB%E6%9B%BC%E7%BC%96%E7%A0%81
  2. 哈夫曼（huffman）树和哈夫曼编码: https://www.cnblogs.com/kubixuesheng/p/4397798.html
  3. word2vec原理(二) 基于Hierarchical Softmax的模型: https://www.cnblogs.com/pinard/p/7243513.html
  4. Decoding a Huffman code with a dictionary: https://stackoverflow.com/questions/33089660/decoding-a-huffman-code-with-a-dictionary
Python
#Huffman树
Huffman树与Huffman编码的Python实现
https://percent4.github.io/Huffman树与Huffman编码的Python实现/
作者
Jclian91
发布于
2024年6月19日
许可协议