NLP（九十九）大模型的数学能力微调及测评

本文将会介绍如何构建数学解题方面数据集，以及对大模型进行微调，并进行数学能力测评。

引言

在文章NLP（九十七）大模型数学解题能力的初步探索中，笔者介绍了对大模型数学解题能力的初步探索，并演示了在微调大约500个样本后，大模型已经初步具备了数学解题的能力。

本文将是上述文章的进一步探索，重点在于如何构造模型训练数据集以及大模型的数学能力测评。

笔者的思路是，首先通过大模型给出数学题的解题思路和解题步骤，然后借助其Python代码生成能力，获得最终答案，即所谓的（Program of Thoughts Prompting, POT）。我们可以先看个例子：

LLM with POT

观察上面的例子，我们可以看到：大模型在解决数学题目的时候，先给出了思考过程，然后是解题步骤，再生成Python代码，执行完Python代码，就能得到最终的正确答案，这就是POT的一个例子，也是笔者希望大模型在解数学题时所执行的完整过程。

从中，我们发现，大模型的分析过程与Python代码是POT的关键步骤，这样能克服大模型不擅长数学计算的缺点，从而提升大模型的数学能力。

在文章NLP（九十七）大模型数学解题能力的初步探索中，笔者也给出了十三个大模型解数学题的例子，都达到了不错的效果。

数据集

接下来谈谈数据集的构造。任何模型，都依赖于高质量的训练数据，因此，构建高质量训练集，是保证模型效果的前提与关键点。

笔者构建大模型数学解题数据集的方法如下：

1. 使用Prompt Engineering（提示工程），让GPT-4生成数学题
2. 使用Gradio构建web服务，利用Few-Shot，人工采集数据并使用GPT-4解题，最后人工检查确认
3. 自动化生成：给定数学题和答案，借助GPT-4及Few-Shot，自动化生成数据集

方案1在文章NLP（九十七）大模型数学解题能力的初步探索中已有介绍，缺点是生成数据不够丰富，效果不够理想，重复数据较多，仍需人工检查，比较费时费力。

方案2需要大量的人工介入，费时费力，但能保证数学题的丰富度，解题质量，可以作为自动化生成方案（即方案3）的补充，会灵活一些。

方案3依赖于现有的数学方面的数据集，需要事先给定数学题和答案，然后利用Few-Shot来约束大模型生成的内容，保证大模型回答的正确性。这种方案可以自动化大规模生成，人工介入极少，且能保证解题质量，缺点是数学习题的丰富度依赖于现成数据集，而这方面的数据集现阶段比较稀缺。

目前，笔者已生成方案1的数据共451条，方案2数据330条，方案3数据1621条，总计2402条数据，且仍在持续更新中。

这里不再详述方案2和3，后面有机会专门介绍。数据集已经开源至Github，网址为：https://github.com/percent4/llm_math_solver .

样例数据如下：

[
    {
        "conversations": [
            {
                "from": "human",
                "value": "题目：苹果的价格是每公斤3元，小明买了2.5公斤的苹果，他一共需要支付多少钱？"
            },
            {
                "from": "gpt",
                "value": "首先给出思考过程：这是一个简单的乘法问题，其中涉及到的是单价和数量的乘积计算。我们需要用苹果的单价乘以小明购买的苹果的重量来找出总金额。\n计算总金额的公式是： \\[ 总金额 = 单价 \\times 数量 \\] 在这个具体例子中，苹果的单价为3元每公斤，小明购买了2.5公斤。\n生成的Python代码如下：\n```python\ndef total_cost(price_per_kg, weight):\n    return price_per_kg * weight\n\n# 苹果的单价（每公斤）\nprice_per_kg = 3\n\n# 小明购买的苹果重量（公斤）\nweight = 2.5\n\n# 计算总金额\ncost = total_cost(price_per_kg, weight)\nprint('小明需要支付的总金额为:', cost)\n```\n"
            },
            {
                "from": "human",
                "value": "现在将上面的代码复制到Python环境中运行，我们应得到小明需要支付的总金额。运行结果将告诉我们具体的金额数值。 运行以上代码，输出会是： ```小明需要支付的总金额为: 7.5```"
            },
            {
                "from": "gpt",
                "value": "因此，小明购买2.5公斤苹果，总共需要支付\boxed{7.5}元。"
            }
        ]
    }
    ...
]

模型微调

我们使用LLaMA-Factory框架对上述数据集进行微调（SFT），使用的基座模型为Qwen1.5-32B模型，微调方式为LoRa, 对话模版使用qwen, 这里不再过多给出细节。

训练完毕后导出模型为Qwen1.5-32B-math，使用下面的命令启动训练后模型的推理服务（兼容OpenAI的API服务）：

CUDA_VISIBLE_DEVICES=0 API_PORT=8000 llamafactory-cli api examples/inference/qwen.yaml

其中qwen.yaml文件配置如下：

model_name_or_path: ./models/Qwen1.5-32B-math
template: qwen
infer_backend: vllm
vllm_enforce_eager: true

数学能力测评

在大模型浪潮的初期，评价大模型的表现一般会采用各种benchmark。而常见的大模型的数学能力测评的benchmark上，所使用的测评数据集为GSM8K和MATH。

GSM8K是大小为8.5K的小学数学数据集，涉及基本算术运算，需要2-8个步骤才能解决，包含7.5K训练集和1K测试集。GSM8K每道题的答案包含完整的解题过程，有助于CoT训练。

MATH是一个包含12500个高中数学竞赛的问题（7500个用于训练，5000个用于测试）的数据集，以文本模式的Latex格式呈现。MATH中的每个问题都有一个完整的逐步解决方案，有助于CoT训练。

当然，现阶段涌现出了更多的测评数据集，比如：GAOKAO(Math), AGIEval, MathQA, Arith3K, TAL-SCQ5K-CN等等，后续有机会将专门介绍大模型的数据能力benchmark. 本文将聚焦在GSM8K和MATH这两个数据集。

我们来看看Qwen1.5官方网站给出的测评结果：

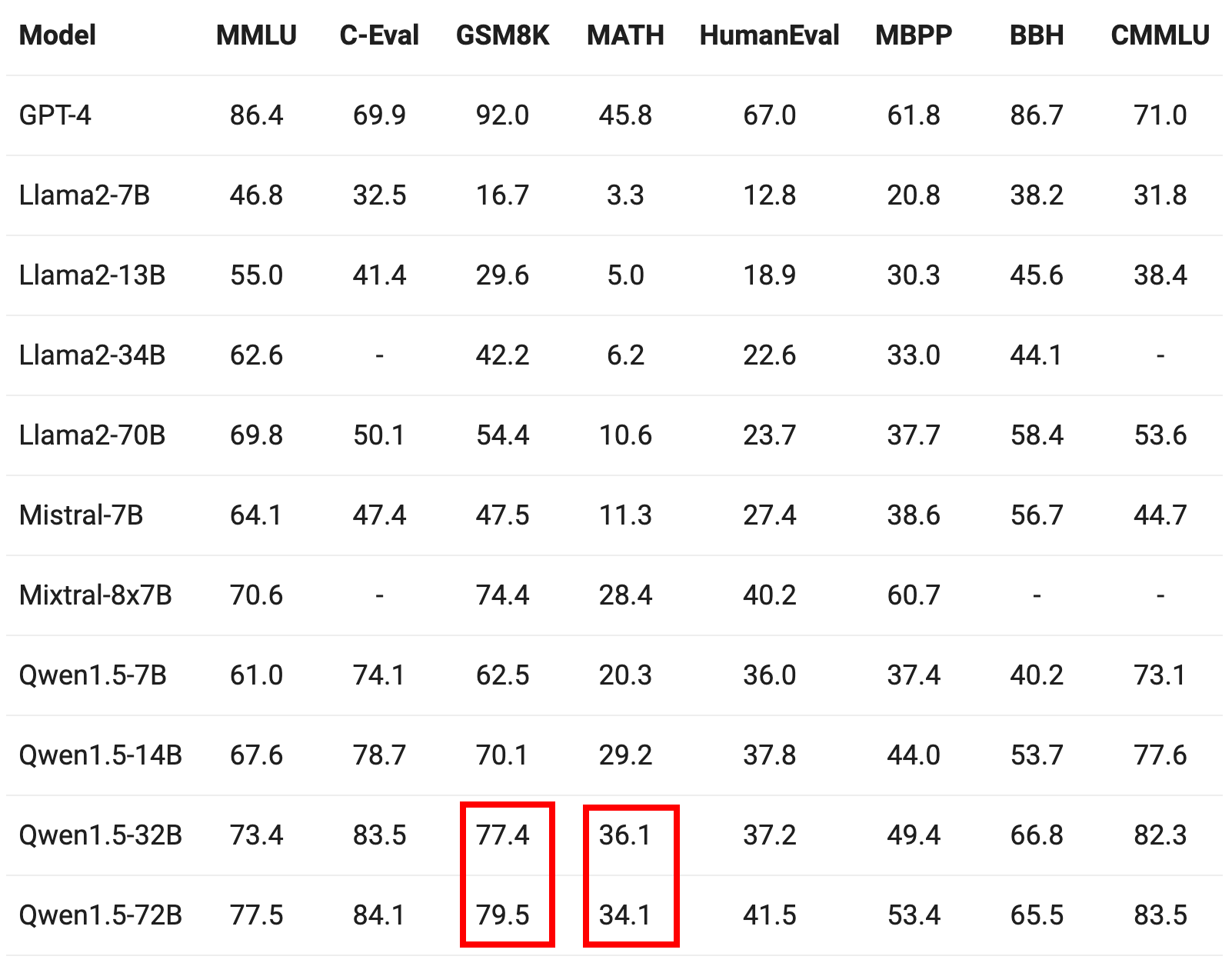
以及0-1万物最新模型给出的测评结果：

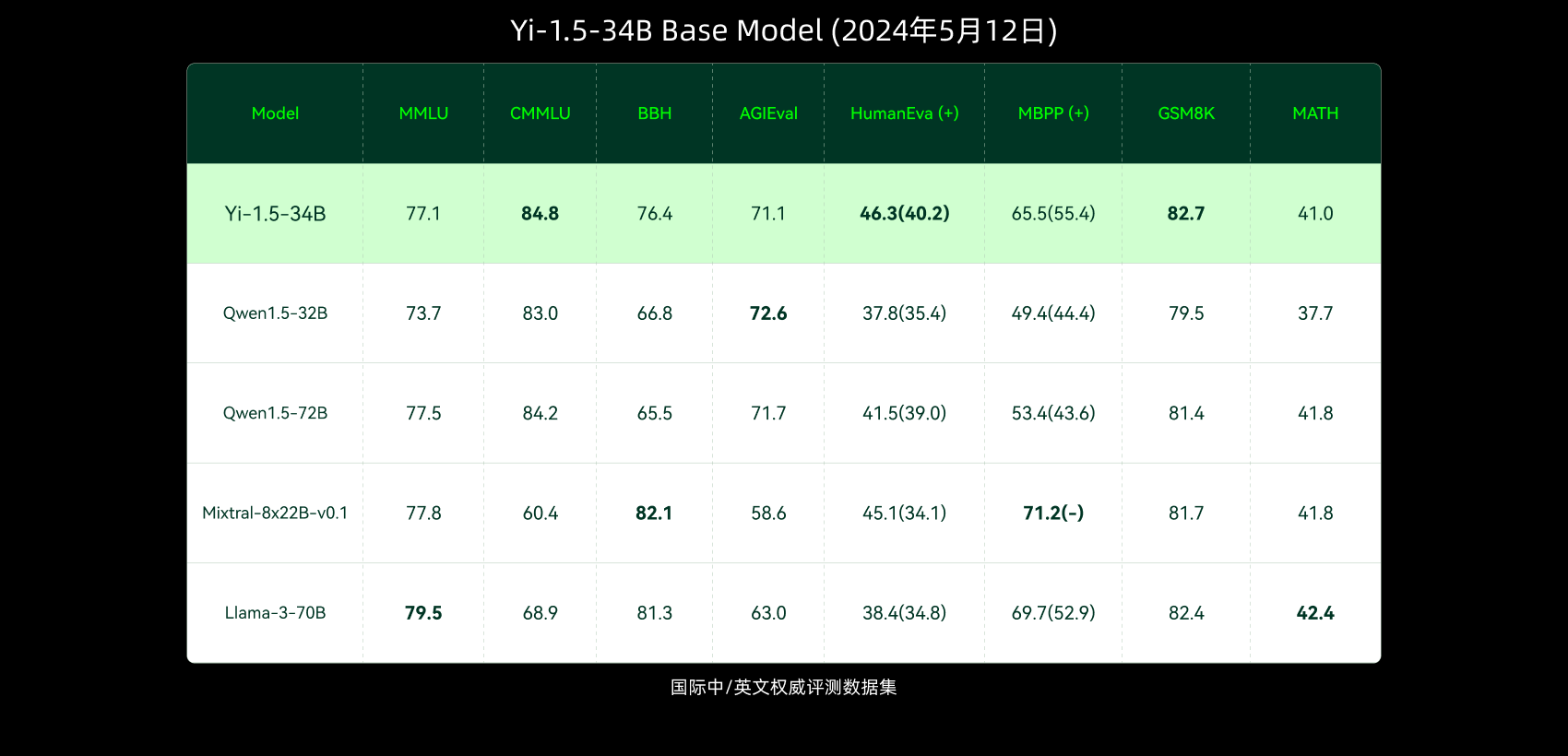
最后是GPT-4o及其同类模型的测评结果：

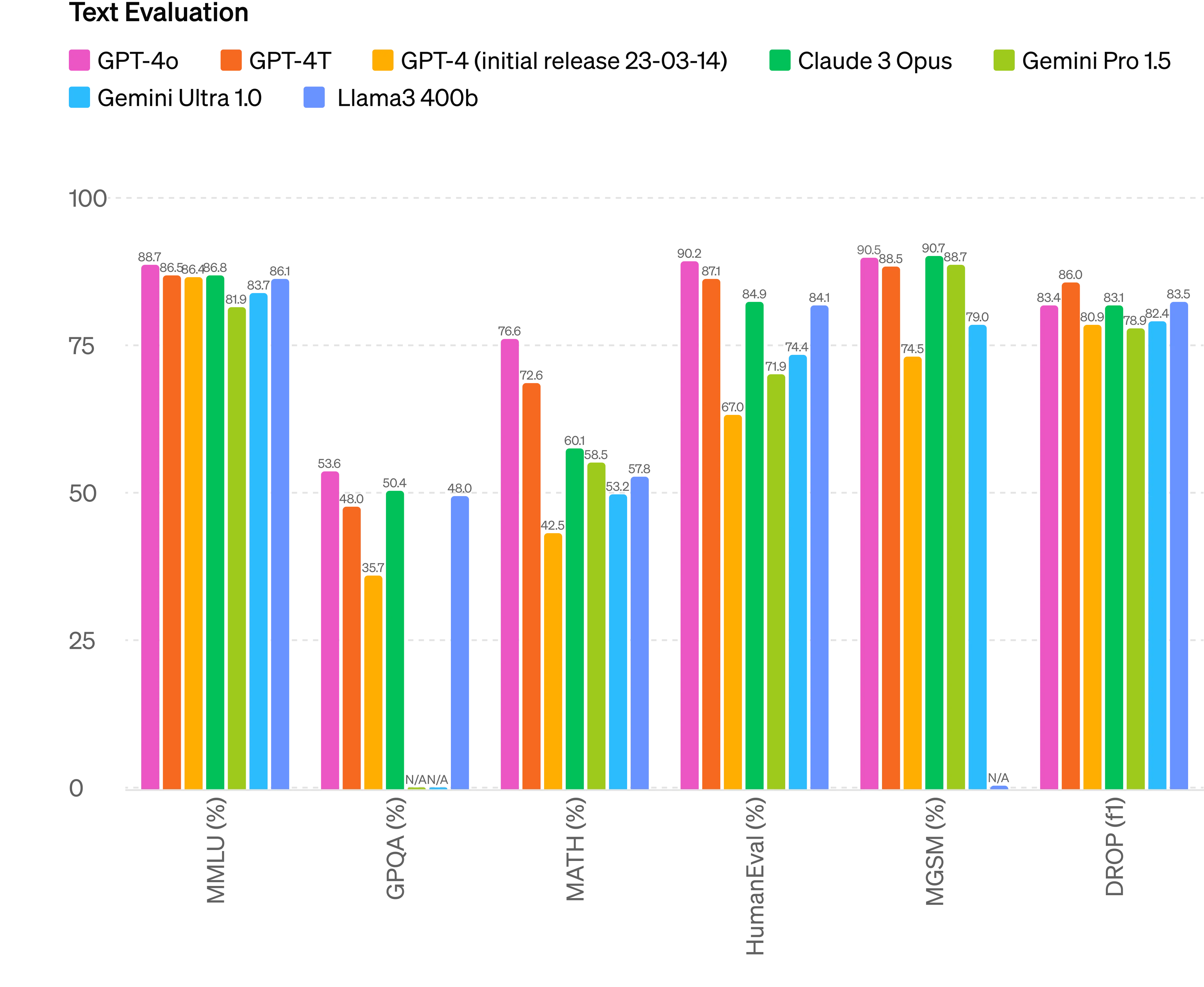
GPT-4o模型在难度很大的MATH数据集上的测评结果已经达到了惊人的76.6%，这是非常亮眼的表现，遥遥领先！

GSM8K测评

回归正题，让我们看看我们微调后的Qwen1.5-32B-math模型的测评结果，首先是GSM8K数据集。

数据集的测评比较困难，在GSM8K数据集中，测试数据的正确答案在 #### 后面，而且一般为整数。而我们微调后的模型，在最后生成的回答中，将正确答案用包围起来，这是参考MATH数据集而标注的样式，这样我们可以直接对比两者的结果，从而给出准确率。

GSM8K数据集的测试集共1319条，我们使用上述的模型推理服务，对这些样本进行预测，得到预测文件。

但有些测评样本的最终答案并没有使用包围起，因此我们需要人工再次确认这些样本。笔者写了一个gradio构建的web页面，用于人工确认，Python代码如下：

# -*- coding: utf-8 -*-
# Human Evaluation for GSM8K
import json
import gradio as gr


def read_samples():
    with open("eval_result.json", "r") as f:
        data = f.readlines()

    content = []
    cnt = 0
    for sample in data:
        sample_dict = json.loads(sample.strip())
        if '\\boxed' not in sample_dict['pred_answer']:
            cnt += 1
            content.append([cnt, sample_dict['question'],
                            sample_dict['answer'].split('####')[-1].strip(),
                            sample_dict['pred_answer'],
                            0])
    return content


def get_human_eval(df):
    # get model evaluation
    with open("eval_result.json", "r") as f:
        data = f.readlines()

    model_true_cnt = 0
    for sample in data:
        sample_dict = json.loads(sample.strip())
        if '\\boxed' in sample_dict['pred_answer'] and sample_dict['is_correct']:
            model_true_cnt += 1
    # get human evaluation
    human_true_cnt = 0
    for i, row in df.iterrows():
        if row['Human Evaluation']:
            human_true_cnt += 1
    return (f"Update {human_true_cnt} samples with human evaluation, \n"
            f"Total Accuracy: {model_true_cnt + human_true_cnt}/{len(data)} = {(model_true_cnt + human_true_cnt)/len(data)}")


with gr.Blocks() as demo:
    with gr.Column():
        with gr.Row():
            table = gr.DataFrame(label='Table',
                                 value=read_samples(),
                                 headers=['No.', 'Question', 'Answer', 'Prediction', 'Human Evaluation'],
                                 interactive=True,
                                 wrap=True)
        with gr.Row():
            output = gr.Textbox(label='Human Evaluation')
            submit = gr.Button("Search")

        submit.click(fn=get_human_eval,
                     inputs=table,
                     outputs=output)

demo.launch()

页面如下：

GSM8K人工确认页面

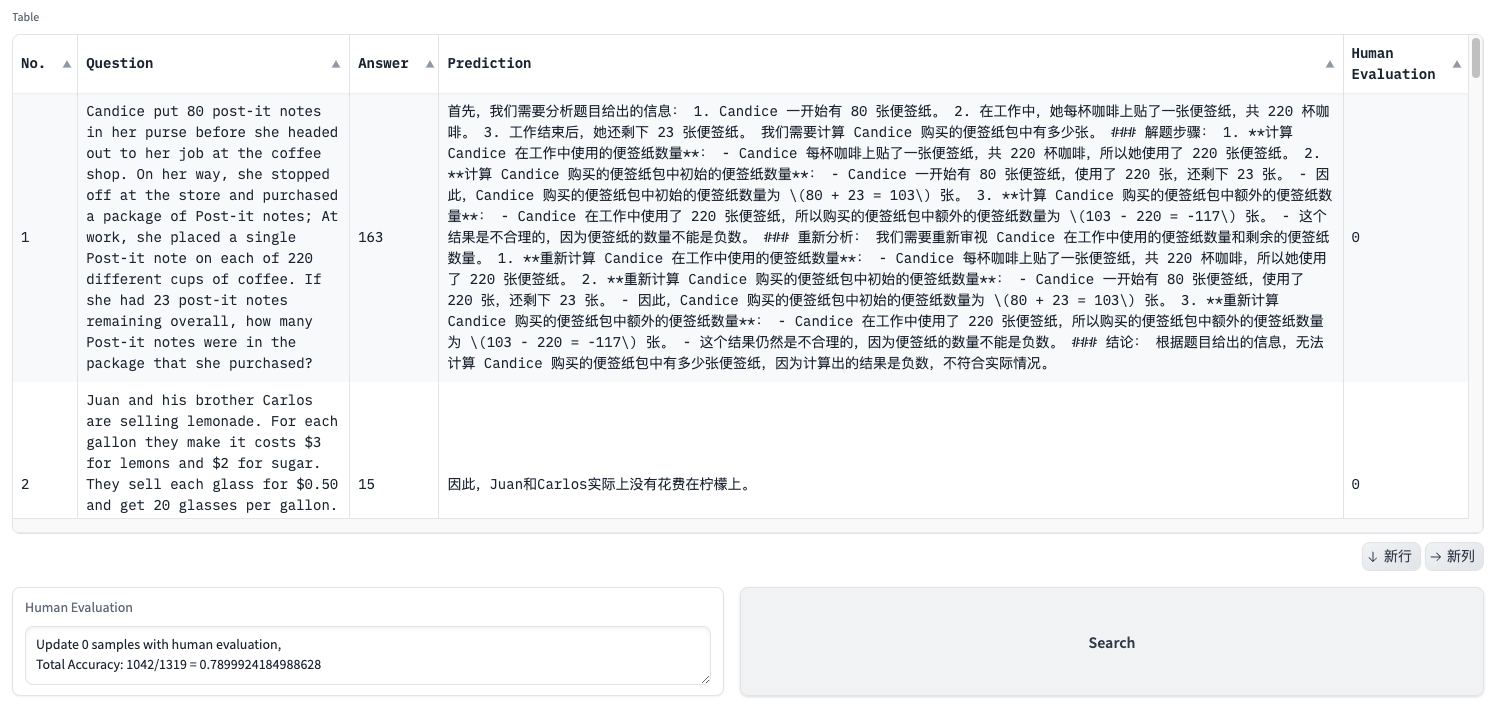
一般，这些需要人工再次确认的样本为10来条。

笔者按照这种方式测评了两次，准确率分为为 79.68% 和 79.4%。

MATH测评

MATH数据集的测评难度较大，一方面其测试集为5000条，题目本身难度大，另一方面，虽然其最终答案用包围起来，与我们微调后的模型一致，但最终答案表述一般比较多变，形式多样，有分数，根式，多项式，整数，小数等等。

在其官网Github项目 hendrycks/math 中，提供了用于判断两个最终答案是否相等的代码脚本 math_equivalence.py ，网址为：https://github.com/hendrycks/math/blob/main/modeling/math_equivalence.py . 笔者对其稍加改造，引入分数与小数是否相等的判断（误差为10^-6）。

使用新的判断标准，测试集上的准确率为39.02%。但这仍然避免不了，有些预测答案与最终答案相等，却被误判了，这是因为笔者构建微调数据集时，执行Python代码得到的是float浮点数，而最终答案一般为分数，根式，或者含pi的表达式等等各种形式，因此，我们还是需要人工确认。

同样地，我们使用Gradio构建人工确认页面，其代码、思路与之前的GSM8K人工确认页面类似，这里不再赘述，有兴趣的读者可参考本文最后给出的Github项目网址。

经过人工再次确认，最终的准确率调整为 43.58% 。 这个结果，超过原生的Qwen1.5-32B模型约7.5个百分点，超过了Qwen1.5-72B模型、Yi-1.5-34B、LLama-3-70B等一种模型，这无疑是对笔者的一个重大激励。但该模型与顶尖的GPT-4o模型仍有非常大的差距！

为了后续的大模型数学解题能力的提升需要，我们需要对这个测评结果进行一些可视化分数，方便我们后续的分析与对比。

• 不同Level回答正确占总的回答正确的占比

• 不同Type回答正确占总的回答正确的的占比

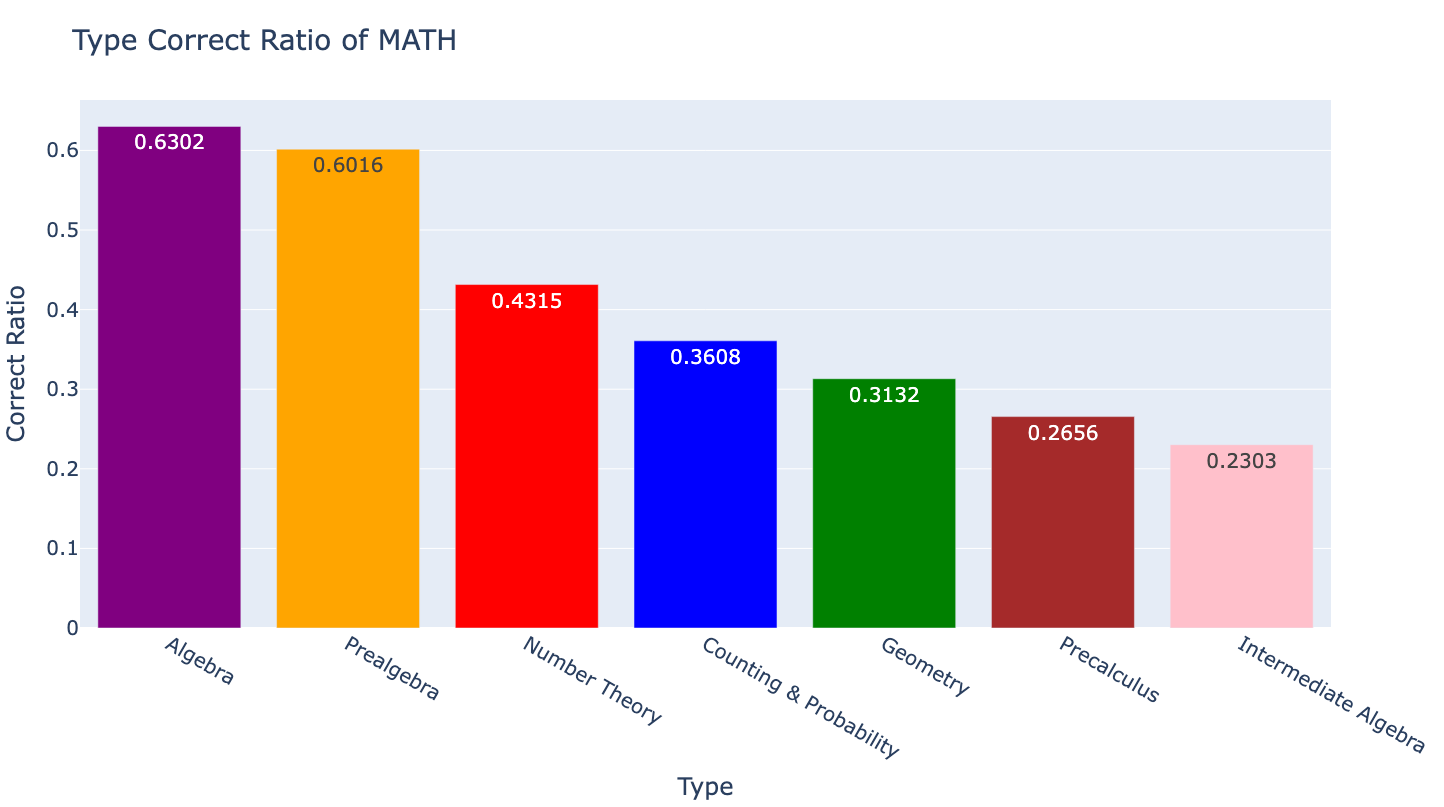
• 不同Type回答正确率条形图

• 不同Level回答正确率条形图

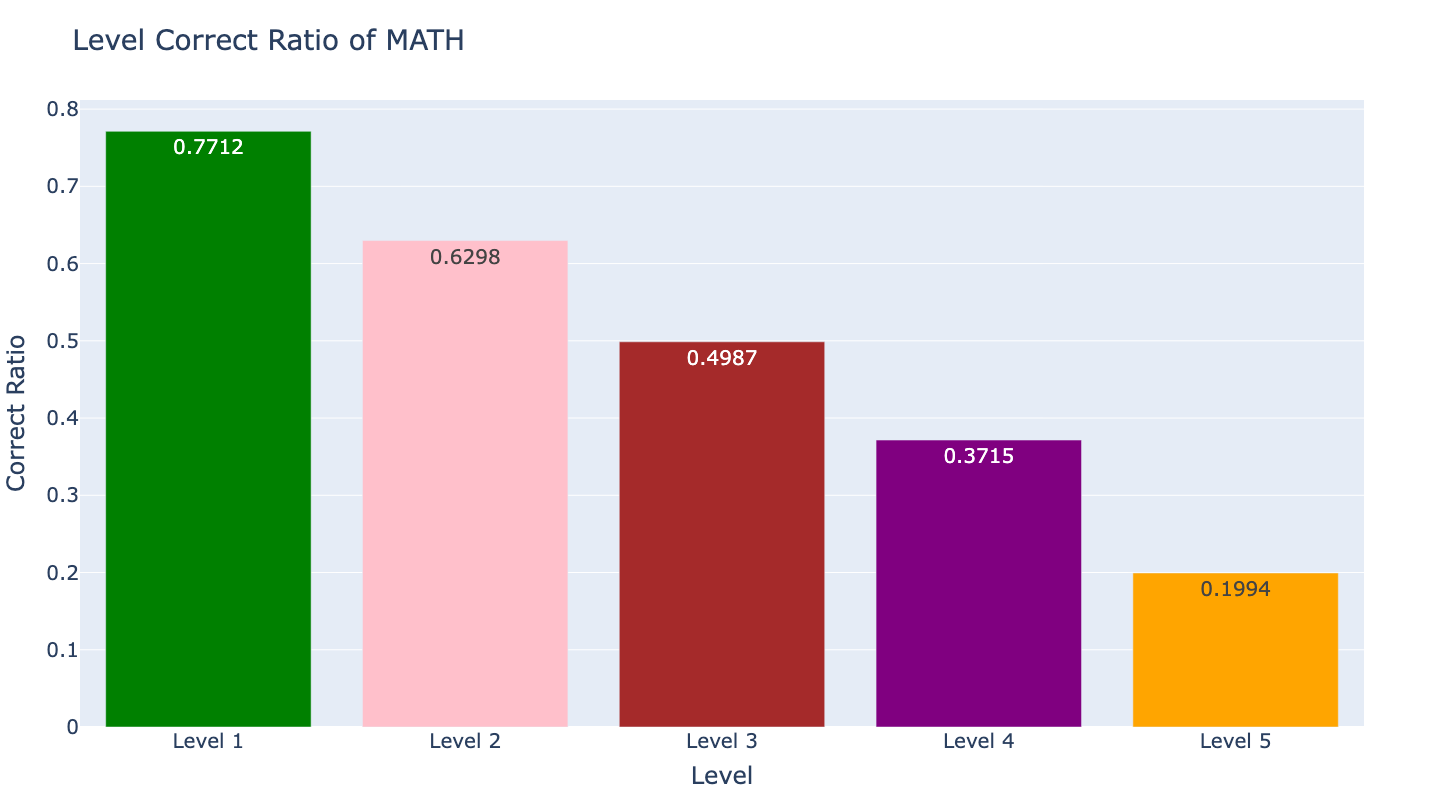
从上述统计图中，我们可以得到很多结论：

• 以回答准确率来说，在Level中以Level 3的贡献最大，在Type中以Algebra的贡献最大。
• 微调后的模型，以Type而言，在Algebra和Prealgebra表现较好，超过了60%，而Precalculus和Intermediate Algebra表现较差，不足30%。
• 微调后的模型，随着Level的上升，其准确率呈阶梯式下降规律，由此可见不同Level的题目对大模型回答准确率的影响。
• ...

总结

本文介绍了如何构建数学解题方面的数据集，以及对大模型进行微调和在GSM8K和MATH数据集上进行测评。

本文凝聚了笔者近一段时间的研究心血，也是后续探索大模型解题能力方向的一个阶段。个人的一点感受是：初步感受大模型的数学解题能力时是非常享受且很有乐趣的一件事，但到后面为了benchmark进行测评时，则是较为痛苦的事情。但你又不能忽视这些benchmark，毕竟，它们是大模型数学能力的重要评估手段。希望后续在这方面有大的提升。

本文给出的数据集、测评方案、Python代码，均已开源至Github，欢迎大家访问~

https://github.com/percent4/llm_math_solver

参考文献

1. Program of Thoughts Prompting: Disentangling Computation from Reasoning for Numerical Reasoning Tasks: https://openreview.net/forum?id=YfZ4ZPt8zd
2. GSM8K: https://matheval.ai/dataset/gsm8k/
3. MATH: https://matheval.ai/dataset/math/
4. Qwen1.5官方网站: https://qwenlm.github.io/zh/blog/qwen1.5/
5. Hello GPT-4o: https://openai.com/index/hello-gpt-4o/
6. 零一万物官网: https://www.lingyiwanwu.com/
7. MathEval 测评数据集: https://matheval.ai/dataset/
8. Measuring Mathematical Problem Solving With the MATH Dataset: https://github.com/hendrycks/math