NLP（四十七）常见的损失函数

本文将给出NLP任务中一些常见的损失函数（Loss Function），并使用Keras、PyTorch给出具体例子。

在讲解具体的损失函数之前，我们有必要了解下什么是损失函数。所谓损失函数，指的是衡量模型预测值y与真实标签Y之间的差距的函数。本文将介绍的损失函数如下：

  • Mean Squared Error（均方差损失函数）

  • Mean Absolute Error（绝对值损失函数）

  • Binary Cross Entropy（二元交叉熵损失函数）

  • Categorical Cross Entropy（多分类交叉熵损失函数）

  • Sparse Categorical Cross Entropy（稀疏多分类交叉熵损失函数）

  • Hingle Loss（合页损失函数）

  • ......

    以下将分别介绍上述损失函数，并介绍Keras和PyTorch中的例子。在此之前，我们分别导入Keras所需模块和PyTorch所需模块。Keras所需模块如下：

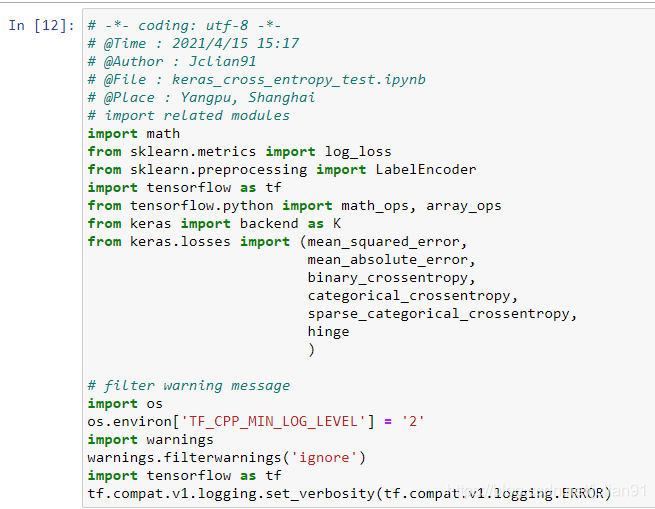
  • 导入Keras相关模块

PyTorch所需模块如下：

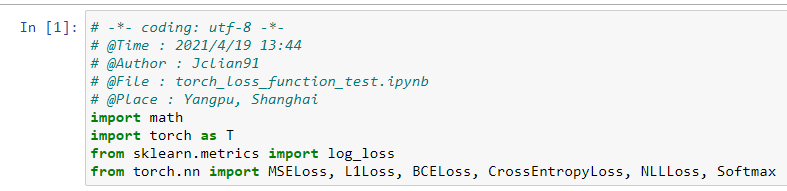
PyTorch所需模块

从导入模块来看，PyTorch更加简洁，在后面的部分中我们将持续比较这两种框架的差异。

Mean Squared Error

Mean Squared Error（MSE）为均方差损失函数，一般用于回归问题。我们用\(\widetilde{y}_{i}\)表示样本预测值序列\(\{\widetilde{y}_{1}, \widetilde{y}_{2},...,\widetilde{y}_{n}\}\)中的第i个元素，用\(y_{i}\)表示样本真实值序列\(\{y_{1}, y_{2},...,y_{n}\}\)中的第i个元素，则均方差损失函数MSE的计算公式如下：

\[MSE=\frac{1}{n}\sum_{i=1}^n(\widetilde{y}_{i}-y_{i})^{2}\]

Keras实现代码如下：

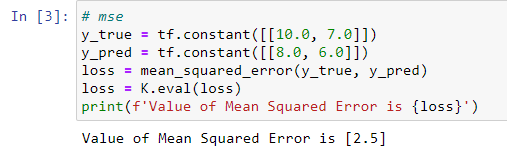
Keras MSE

PyTorch实现代码如下：

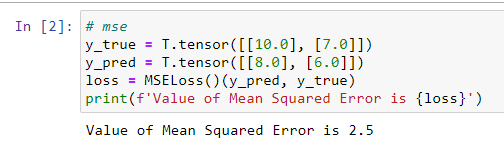
PyTorch MSE

Mean Absolute Error

Mean Absolute Error（MAE）为绝对值损失函数，一般用于回归问题。我们用\(\widetilde{y}_{i}\)表示样本预测值序列\(\{\widetilde{y}_{1}, \widetilde{y}_{2},...,\widetilde{y}_{n}\}\)中的第i个元素，用\(y_{i}\)表示样本真实值序列\(\{y_{1}, y_{2},...,y_{n}\}\)中的第i个元素，则绝对值损失函数MAE的计算公式如下：

\[MAE=\frac{1}{n}\sum_{i=1}^n|\widetilde{y}_{i}-y_{i}|\]

Keras实现代码如下：

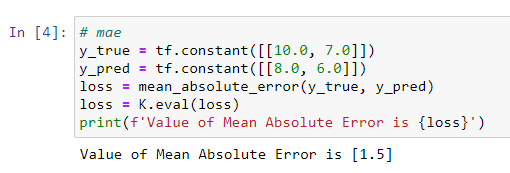
Keras MAE

PyTorch实现代码如下：

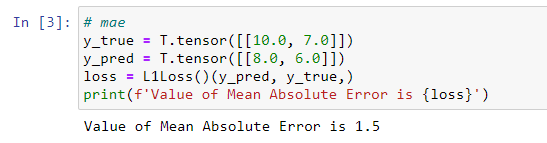
PyTorch MAE

注意，在PyTorch中L1Loss中的L1表示为L1范数，即通常所说的绝对值，绝对值函数\(|x|\)处处连续，但在x=0处不可导。

Binary Cross Entropy

Binary Cross Entropy（BCE）为二元交叉熵损失函数，一般用于二分类问题。我们用Y表示样本真实标签序列（每个值为0或者1），用\(\bar{Y}\)表示样本预测标签序列（每个值为0-1之间的值），则BCE计算公式如下：

\[BCE=Y \cdot (-log(\bar{Y}))+(1-Y) \cdot (-log(1-\bar{Y}))\]

我们不在讲解具体的计算公式，如需具体的计算方式，可以参考文章Sklearn中二分类问题的交叉熵计算。

Keras实现代码如下：

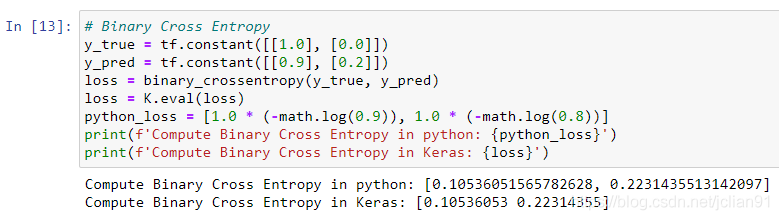
Keras BCE

PyTorch实现代码如下：

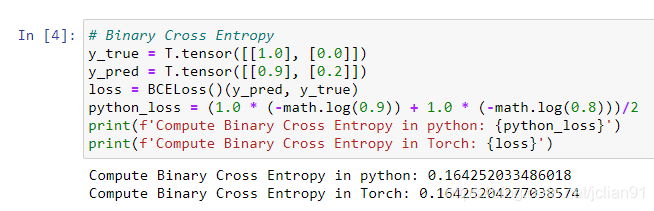
PyTorch BCE

从上面的结果中可以看到Keras和PyTorch在实现BCE损失函数的差异，给定样本，Keras给出了每个样本的BCE，而PyTorch给出了所有样本BCE的平均值。更大的差异体现在多分类交叉熵损失函数。

Categorical Cross Entropy

Categorical Cross Entropy（CCE）为多分类交叉熵损失函数，是BCE（二分类交叉熵损失函数）扩充至多分类情形时的损失函数。多分类交叉熵损失函数的数学公式如下：

\[CCE=-\frac{1}{N}\sum_{i=1}^{N}\sum_{c=1}^{C}1_{y_{i}\in C_{c}}log(p_{model}[y_{i}\in C_{c}])\]

其中N为样本数，C为类别数，\(1_{y_{i}\in C_{c}}\)表示第i个样本属于第c个类别的值（0或1），\(p_{model}[y_{i}\in C_{c}]\)表示模型预测的第i个样本属于第c个类别的概率值（0-1之间）。如需查看具体的计算方式，可以参考文章多分类问题的交叉熵计算。

Keras实现代码如下：

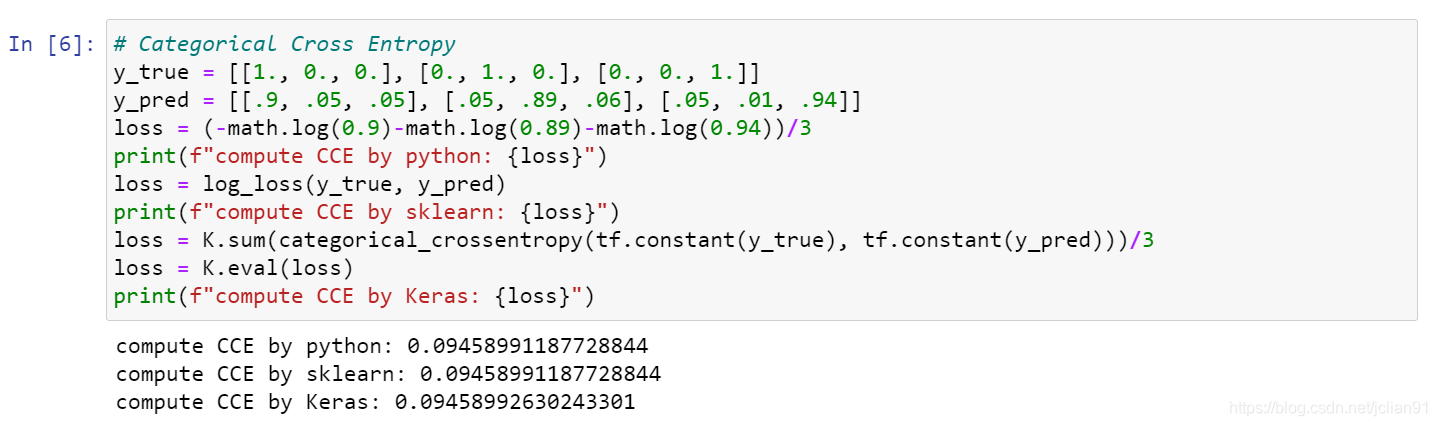
Keras CCE

PyTorch中的CCE采用稀疏多分类交叉熵损失函数实现，因此直接查看稀疏多分类交叉熵损失函数部分即可。

Sparse Categorical Cross Entropy

Sparse Categorical Cross Entropy（稀疏多分类交叉熵损失函数，SCCE）原理上和多分类交叉熵损失函数（CCE）一致，属于多分类问题的损失函数，不同之处在于多分类交叉熵损失函数中的真实样本值用one-hot向量来表示，其下标i为1，其余为0，表示属于第i个类别；而稀疏多分类交叉熵损失函数中真实样本直接用数字i表示，表示属于第i个类别。

Keras实现代码如下：

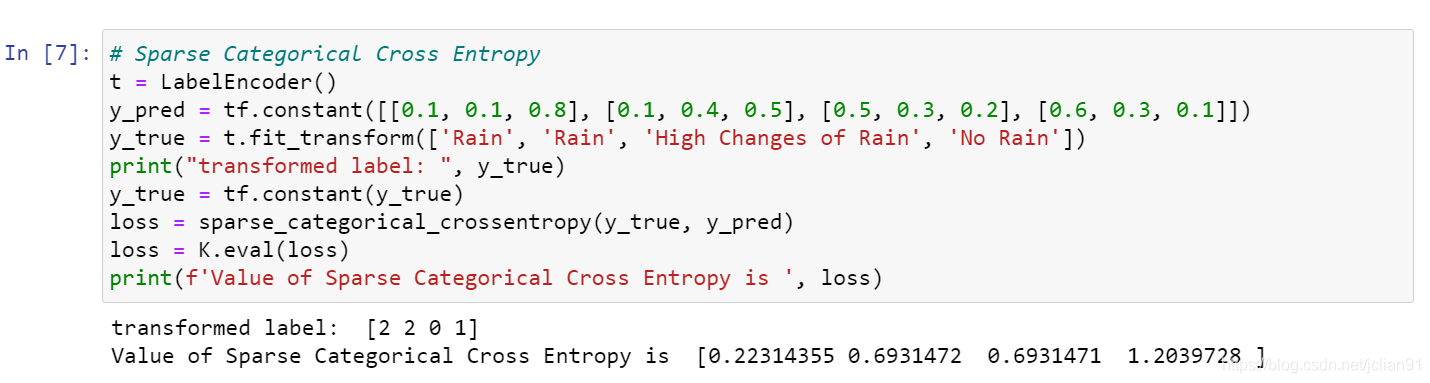
Keras SCCE

例子中一共四个样本，它们的真实样本标签为[2,2,0,1]，不是one-hot向量。

PyTorch中的SCCE实现代码与上述数学公式不太一致，有些微改动。我们先看例子如下：

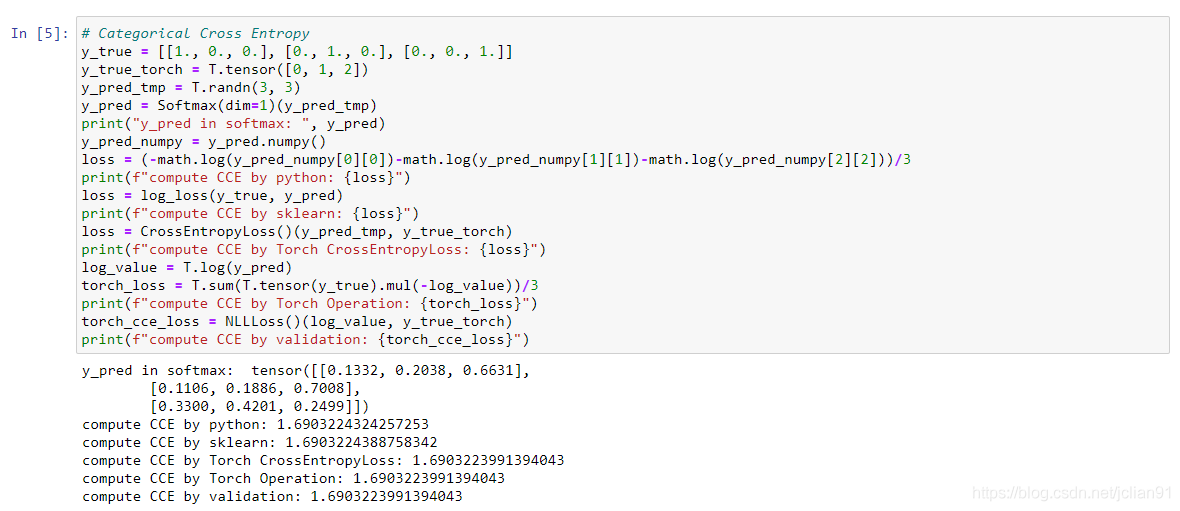
PyTorch SCCE

这明显与Keras实现代码是不一致的。要解释这种差别，我们就要详细了解PyTorch是如何实现CCE损失函数的。

简单来说，PyTorch中的输入中的样本预测，不是softmax函数作用后的预测概率，而是softmax函数作用前的值。对该值分别用softmax函数、log函数、NLLLoss()函数作用就是PyTorch计算SCCE的方式。

在上面的例子中，y_pred_tmp是softmax函数作用前的值，是PyTorch计算SCCE的预测样本的输入，y_pred是softmax函数作用后的值，是sklearn模块、Keras计算SCCE的预测样本的输入。对y_pred_tmp、y_true使用softmax函数、log函数所得到的结果，与y_pred、y_true使用sklearn模块、Keras计算SCCE的结果一致，而对该结算结果再作用NLLLoss()，就是PyTorch计算SCCE的方式。

也许上面的解释还有点模糊，我们借助知乎上别人给出的一个例子也许能更好地理解PyTorch计算SCCE的方式，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# -*- coding: utf-8 -*-
import torch
import torch.nn as nn
x_input = torch.randn(3, 3)   # 随机生成输入
print('x_input:\n', x_input)
y_target = torch.tensor([1, 2, 0])    # 设置输出具体值 print('y_target\n',y_target)

# 计算输入softmax，此时可以看到每一行加到一起结果都是1
softmax_func = nn.Softmax(dim=1)
soft_output = softmax_func(x_input)
print('soft_output:\n', soft_output)

# 在softmax的基础上取log
log_output = torch.log(soft_output)
print('log_output:\n', log_output)

# 对比softmax与log的结合与nn.LogSoftmaxloss(负对数似然损失)的输出结果，发现两者是一致的。
logsoftmax_func = nn.LogSoftmax(dim=1)
logsoftmax_output = logsoftmax_func(x_input)
print('logsoftmax_output:\n', logsoftmax_output)

# pytorch中关于NLLLoss的默认参数配置为：reducetion=True、size_average=True
nllloss_func = nn.NLLLoss()
nlloss_output = nllloss_func(logsoftmax_output, y_target)
print('nlloss_output:\n', nlloss_output)

# 直接使用pytorch中的loss_func=nn.CrossEntropyLoss()看与经过NLLLoss的计算是不是一样
crossentropyloss = nn.CrossEntropyLoss()
crossentropyloss_output = crossentropyloss(x_input, y_target)
print('crossentropyloss_output:\n', crossentropyloss_output)

输出结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
x_input:
 tensor([[ 0.1286,  1.1363,  0.5676],
        [ 1.0740, -0.7359, -0.6731],
        [ 0.7915, -0.8525, -1.2906]])
soft_output:
 tensor([[0.1890, 0.5178, 0.2932],
        [0.7474, 0.1223, 0.1303],
        [0.7588, 0.1466, 0.0946]])
log_output:
 tensor([[-1.6659, -0.6582, -1.2269],
        [-0.2911, -2.1011, -2.0382],
        [-0.2760, -1.9200, -2.3581]])
logsoftmax_output:
 tensor([[-1.6659, -0.6582, -1.2269],
        [-0.2911, -2.1011, -2.0382],
        [-0.2760, -1.9200, -2.3581]])
nlloss_output:
 tensor(0.9908)
crossentropyloss_output:
 tensor(0.9908)

Hingle Loss

Hingle Loss为合页损失函数，常用于分类问题。合页损失函数不仅要分类正确，而且确信度足够高时损失才是0，也就是说，合页损失函数对学习有更高的要求。一个常见的例子为SVM，其数学公式如下：

\[Hingle Loss=max(0, 1-y \cdot \widetilde{y})\]

其中\(y\)为真实标签，\(\widetilde{y}\)为预测标签。

Keras实现代码如下：

Keras Hingle Loss

PyTorch中没有专门的Hingle Loss实现函数，不过我们可以很轻松地自己实现，代码如下：

PyTorch Hingle Loss

总结

本文介绍了NLP任务中一些常见的损失函数（Loss Function），并使用Keras、PyTorch给出具体例子。

本文代码已上传至Github，地址为：https://github.com/percent4/deep_learning_miscellaneous/tree/master/loss_function 。

2021年4月24日于上海浦东，此日惠风和畅~

参考网址

  1. How To Build Custom Loss Functions In Keras For Any Use Case：https://cnvrg.io/keras-custom-loss-functions/
  2. Pytorch常用的交叉熵损失函数CrossEntropyLoss()详解：https://zhuanlan.zhihu.com/p/98785902
欢迎关注我的公众号NLP奇幻之旅，原创技术文章第一时间推送。

欢迎关注我的知识星球“自然语言处理奇幻之旅”，笔者正在努力构建自己的技术社区。

NLP
#NLP #损失函数
NLP（四十七）常见的损失函数
https://percent4.github.io/NLP（四十七）常见的损失函数/
作者
Jclian91
发布于
2023年7月10日
许可协议