MATH Eval

MATH 数据集评测

MATH是一个包含12500个高中数学竞赛的问题（7500个用于训练，5000个用于测试）的数据集，以文本模式的Latex格式呈现。MATH中的每个问题都有一个完整的逐步解决方案，有助于CoT训练。

模型预测

MATH数据集的测试集共5000条，我们使用上述的模型推理服务，对这些样本进行预测，得到预测文件，推理过程较为漫长，在笔者单卡A100上需要大概1半天的时间。

预测脚本如下：

eval/MATH/MATH_eval.py: evaluation script for MATH dataset

可以看到，该预测脚本与上述的GSM8K测评大致相同，只是缺少了准确率统计步骤。这是因为，MATH测试集的最终答案虽然用\boxed{}包围起来，但表达形式多样，且有些较为复杂，包含根式，分数，含pi表达式，多项式，区间等等。当然，微调模型的最终答案也用\boxed{}包围起来。

因此，如何判定预测答案与标准答案是否一致，这是一件困难的事情。

答案一致判定

在Github项目 hendrycks/math 中，提供了用于判断两个最终答案是否相等的代码脚本 math_equivalence.py ，网址为：https://github.com/hendrycks/math/blob/main/modeling/math_equivalence.py . 笔者对其稍加改造，引入分数与小数是否相等的判断（误差为10^-6），代码如下：

eval/MATH/math_equivalence.py: check whether two answer are equal in math

对上述判定代码进行单元测试，测试脚本如下：

eval/MATH/math_equivalence_test.py: unittest for math equivalence.

使用命令python3 -m unittest MATH/math_equivalence_test.py -v运行上述单元测试，一共22个测试case，均测试通过。

初步准确率

利用上述答案一致判定方法，我们对微调模型预测后的文件进行初步的准确率统计，Python代码如下：

eval/MATH/math_eval_update.py: update the evaluation result with correctness for MATH dataset.

运行上述代码，得到初步准确率为47.84%。

人工确认

当然，和GSM8K数据集一样，我们需要对两边答案不一致的预测样本进行人工确认，因为上述的数学答案一致判定并不能覆盖所有的场景。

人工确认的Python代码如下：

eval/MATH/human_eval_server.py: human check script for MATH dataset using Gradio.

经人工确认，最终微调后的Yi-1.5-34B-math模型在MATH测试集上的准确率修正为52.76%，其中包含预测错误样本共89个。

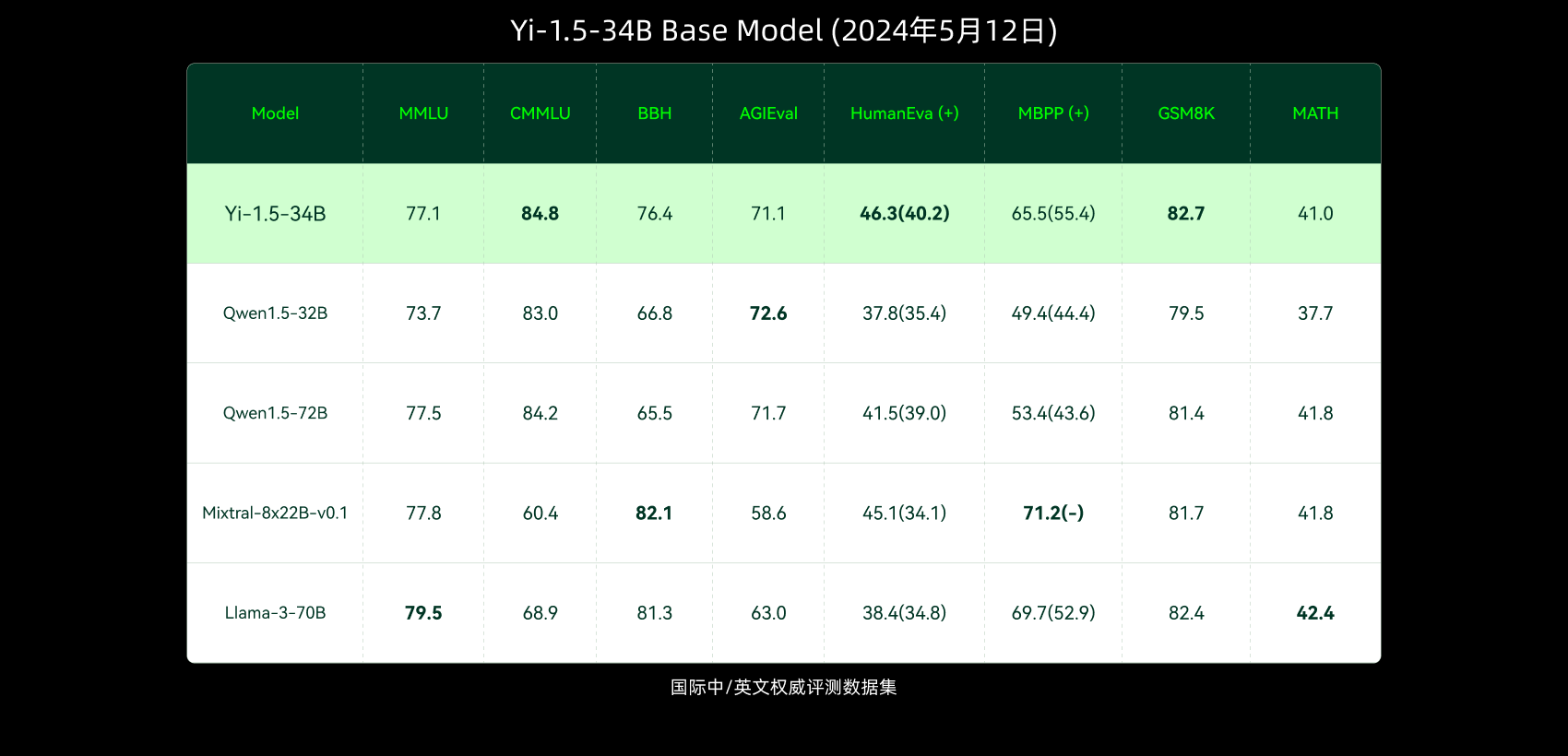
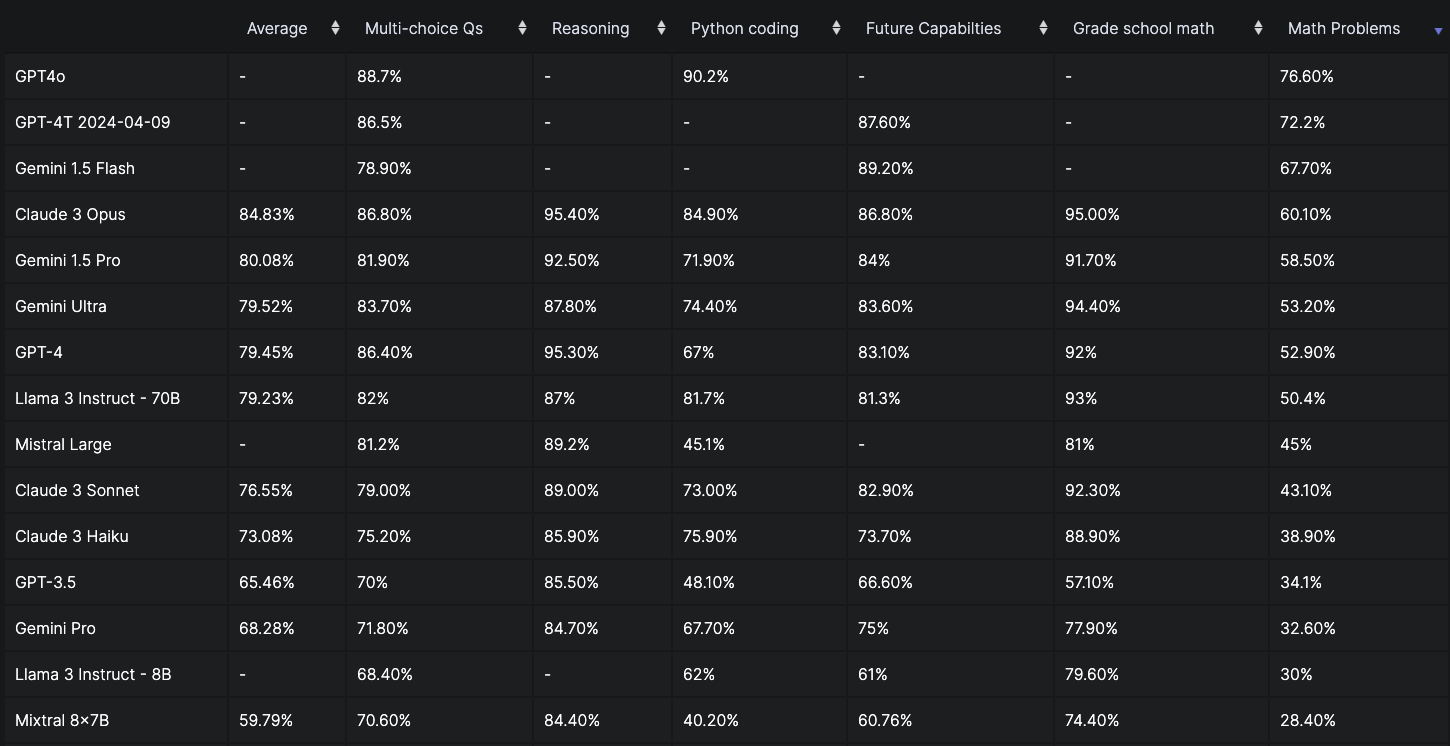
在MATH测试集的准确率方面，Yi-1.5-34B-math模型超过原生Yi-1.5-34B模型11.76个百分点，超过微调Qwen1.5-32B-math模型9.18个百分点，且非常接近初版GPT-4模型的准确率（52.90%）。